FRIDAY, 25 JANUARY 2013
From the puzzling works of M. C. Escher to the grand architecture that rises above our cities, the deep relation between geometry and art underlies a lot of what we find beautiful. The artistic construction of geometric ideas has inspired breakthroughs in mathematics, cosmology and physics, and conversely, ideas from geometry are applied in modern art to construct images that we find naturally beautiful. Many mathematicians and physicists believe that beauty is an indicator of truth when it comes to the equations that govern our world.The most defining example of this interaction can be found in the work of M.C. Escher, a Dutch artist of the early twentieth century. Escher combined his appreciation of geometry with his creativity to construct works of art that fool our mind’s sense of space, creating pieces of great intrigue and beauty.
M. C. Escher was born in Leeuwarden, in the Netherlands in 1898. He was a sickly child, who failed to excel at school, despite obvious artistic talents. In 1919, he went to art college. He was briefly a student of architecture, but quickly changed to the decorative arts, having realised that life as an architect was not for him. Escher produced his first notable work in 1937, inspired by the mathematical, geometric shapes he had seen while travelling through Spain and Italy. He kept records of mathematics in his notebooks, which he hoped would help him to forge a union between mathematics and his art. Geometry was a great inspiration to Escher, and many of his artworks are based on intricate geometric shapes. But do we really understand what we are seeing when we are struck by the beauty of Escher’s artwork?
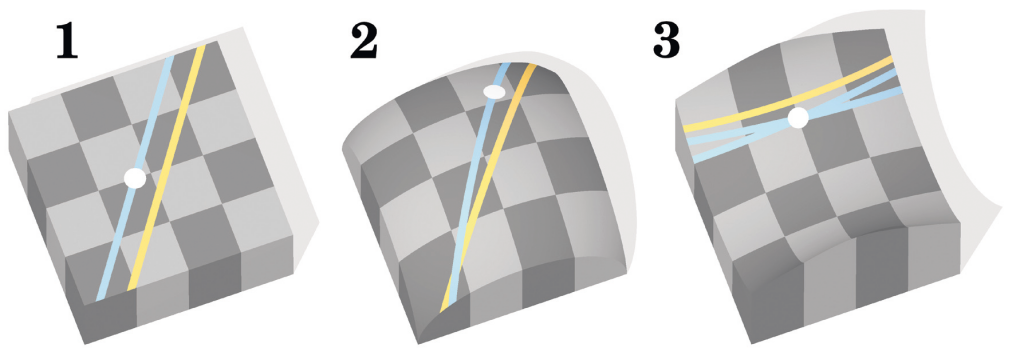
Geometry is the study of the relationships between lines, points and surfaces. It is the mathematics of shapes. Whether we know it or not, we are all familiar with what’s called Euclidean geometry, with its straight lines, angles, and circles, studied in maths classes around the world. Euclid stated five rules from which all other results can be derived. One of these is the Parallel Postulate, which states that given any line we will always be able to draw exactly one parallel line through a point not on the given line.
But we can relax the Parallel Postulate, constructing new geometries which differ to Euclidean geometry, each with their own intrinsic beauty. If we have no parallel lines, then we can build what is known as elliptic geometry. Alternatively, if more than one parallel line can be drawn, we can construct a hyperbolic geometry.
Elliptic geometry is best understood by imagining the surface of a sphere. As our geometry has changed, our definition of what a straight line will be must change. Imagine the path of an aeroplane around the globe. In elliptic geometry, this is what straight lines are like. Straight lines are represented as equatorial circles wrapped around the sphere. Aircraft follow these equatorial circles when flying across the globe, as they are the shortest distance between two points on the sphere. Many of Escher’s works help to visually illustrate the differences between elliptic geometry and Euclidean geometry. The differences were ones he made use of artistically, to create new and innovative patterns such as in the bulging section of his work: Balcony.
In contrast, hyperbolic geometry cannot be thought of in terms of aeroplanes and the Earth’s surface. Instead, we can represent the entire hyperbolic space as the interior of a circle in the Euclidean plane. In other words, the interior of what you think of as a normal 2D circle. The boundary of the circle represents infinity. Straight lines are represented by either an arc of a circle which meets the boundary at right angles, or a straight line through the centre. After discussions with geometer H.S.M. Coxeter, Escher produced the beautiful Circle Limit I. Escher highlights some of the straight lines in this geometry, which coincide with the spines of the fish. A square in this geometry has angles which sum to less than the angles of a square in Euclidean geometry. All of the fish are the same size in the hyperbolic geometry, yet in this representation in a Euclidean plane they have been distorted and appear smaller.
Not only is hyperbolic geometry beautiful, it also has physical applications. When formulating his laws of relativity, Einstein’s great insight was that nothing can travel as fast as the speed of light. Suppose we conduct our own thought experiment, as Einstein did: What happens if you’re flying at half the speed of light, relative to someone standing still, and you throw a shotput out in front of you at half the speed of light again? Surely the observer would see the shotput travelling at the speed of light, but Einstein’s insight was that nothing could travel as fast as the speed of light, so either we’re wrong, or Einstein was wrong.
Unsurprisingly, it’s not Einstein, although the explanation as to why we are wrong requires help from hyperbolic geometry. Inside the hyperbolic geometry of Escher’s Circle Limit I, each fish is the same size, so adding two fishes end to end gives two fish lengths. But from outside the hyperbolic geometry, the Euclidean length is less than two fish lengths. If the addition of speeds functioned according to hyperbolic geometry, say by letting one hyperbolic-fish length represent half the speed of light, then from our exterior Euclidean perspective the total speed of the shotput is still less than the speed of light. So Einstein was right.
Hyperbolic geometry has a huge range of uses other than inspiring art and explaining relativity. But there’s another question we would like to ask - what type of geometry does our universe have, on a cosmological scale? Euclidean geometry might be enough to tell you the distance to the shops, or even the length of a train journey. But if we go up a scale, to the geometry of planet Earth, we see we need spherical geometry. If we go up another scale, to the universe as a whole, we lose our ability to make assumptions altogether. We can’t just assume the universe is totally flat and Euclidean; perhaps it exhibits spherical geometry, or the beautiful hyperbolic geometry above. This is one of the unresolved problems of cosmology, and physicists are conducting research to determine the curvature of the universe as a whole. Possibly surprisingly, so far the signs show the universe seems more or less Euclidean, but with advancements in technology allowing us to see ever further into space, who knows what shape the universe will eventually reveal itself to be.
Zac Kenton is a 4th year undergraduate studying Mathematics
All M.C. Escher works © 2010 The M.C. Escher Company - the Netherlands. All rights reserved. Used by permission. www.mcescher.com